3.6 Midpoint Displacement Method
The mathematical, non-linear and linear fractals presented above are deterministic, which means that repeating the transformations under the same starting conditions will always result in the same figures. The midpoint displacement method, however, belongs to the category of random fractals, such as the fractals generated by the DLA-method, which in general produce more nature-like "random" objects.
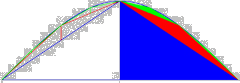
How does the Midpoint displacement method works? We draw a triangle on the screen and mark the centers of the three borderlines. Then we move these points perpendicularly to the lines up or down by a random factor. The resulting object consists of four smaller triangles, one of them is the combination of the three newly constructed points - see picture 20. The same is applied to the new triangles, and so on. For the decision whether the center point is moved up or down we use a coin. If the values of the displacement, the vertical intervals, decrease slowly, the resulting object will look like a "young" highly rugged mountain. In contrast to that, any fast decreasing of the displacement factor after only a few iterations produces a smooth mountain.