3.4 DLA Models - Diffusion-Limited Aggregation Model

In physics and chemistry diffusion means a certain behavior of two different gases or liquids, which get in touch with each other. This behavior is characterized by the circumstance that two different gases or liquids are mixed when they are brought together. This mixture happens because of molecular heat emission, but the way of diffusion, its “form”, cannot be forecast, which means that it cannot be calculated by mathematics.

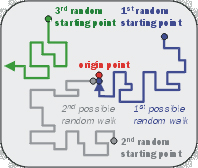
How can diffusion then be described? Through simulation: a certain point is marked, for example in the middle of the computer-screen. This point is the starting point of the diffusion. Now another point, anywhere on the screen starts its wanderings. The way it follows is random, analogous to the Brown's movement[01] . The movement is stopped when it touches the stationary point, because at that moment it is also turned into a fixed point. We can also think of a screen full of dead cells - one cell of which is turned to life in the middle part of the screen. Touching this living point means that the moving cell is also turned to life. The random movement is repeated for the next cell or point anywhere on the screen - see picture 18.

The developing object looks like a map of bigger streets with some dead end roads. There are two extreme cases for possible starting points: first, the point lies in between those streets which means that the moving point would quickly be fixed at the nearest street and therefore the random walk would be very short. Second, the starting point could also lie on an already living cell, which means that no random walk is possible. In both cases the random possibilities of the walk are highly restricted, therefore the only limit of the simulation is that the new point must not be chosen inside the growing object. In a computer simulation program this can be avoided by drawing a circle with the largest extension of the object. The new starting points then have to be chosen outside this circle[02].

Footnotes

[01] Brown movement: when we look at a glass of fluid which is in balance it seems that all particles are immovable. Now if we put any tiny object into the fluid, this object will sink to the ground and will stay there without moving. If this object is a heavy ball it will sink vertically and will not come up again. This is true for objects we can see and we are used to. When we zoom more closely to the fluid with the help of a microscope and put some little particle in the fluid we will see another phenomenon: observing it we will see that the particle does not sink down vertically but moves up and down without any order, rotates without resting. Drawing the way on a paper we can define the position of the particle every e.g. 30seconds and connect them by straight lines. In each of these points a tangent can be drawn, but in reality the particle moves in between, too. That means that the tangents are only true for the curve of "every 30 seconds" and not for the real course. Beside that the way of the Brown-movement nearly fills the plane - this would mean that the way of the Brown-movement is topologically a curve of the dimension 1, but because it nearly fills the plane it is a fractal of higher dimension. Mandelbrot Benoit B., Dr. Zähle Ulrich (editor of the german edition), Die fraktale Geometrie der Natur (1991) einmalige Sonderausgabe, Birkhäuser Verlag Berlin, ISBN 3-7643-2646-8, p.24.
[02] Voß Herbert, Chaos und Fraktale - selbst programmieren (1994), Franzis-Verlag GmbH Österreich, ISBN 3-7723-7003-9, p.92.