3.3 IFS - Iteration Function Systems

Iterated function systems, the so-called IFS, again belong to the types of linear fractals like the true mathematical fractals. They are produced by polygons that are put in one another and show a high degree of similarity to nature - such as the fern presented in picture 15. The IFS form the connection between the true mathematical fractals and nature[01] .

The IFS can be illustrated with the Sierpinski Gasket by its insertion-rules, remember the copy machine of picture 02: a “starting”-square is replaced by three squares of half-size, one situated on the middle top, the other two on the left and right bottom. In the next step each of the three squares is replaced by another three shorter squares and so on. It is not the starting image, in this case a square that influences the resulting picture but the rules itself - see picture 16. The only difference lies in the detail, zooming in on the object will show the different starting objects, except after infinite iterations when those single objects turn to infinitely small ones. In the IFS, the transformation rules can also include rotation, reduction, enlargement, shear and similar rules, which are described in mathematics as affine linear transformations - see chapter “2.2.2 Characteristics - A Fractal is Self-Similar”. For each single lens or single insertion rule these transformation rules can be chosen differently.

It will require many iterations, runs of insertions, until the single objects, e.g. the rectangles of Barnsley's fern shown in picture 15, cannot be identified any more. In the case of the fern this will take about 50 iterations, which means that rectangles have to be drawn - , with “n” number of transformations, “m” number of iterations and “N” number of elements of the resulting object after “m” iterations[02] . Generating these 50 iterations takes a lot of time even with the assistance of the computer, therefore another method is chosen to get the resulting fern, the so-called "chaos game" - see picture 17, an explanation is also given at picture 09 “Sierpinski Gasket”. In that case the four insertion-rules are expressed by four mathematical affine transformations[03] of the form
.
For IFS these transformations must be contractions, which are reached in the way, that A, B, C, and D remain within the range of -1 and +1. An IFS always consists of more than one contraction function , e.g. four functions are given for the so-called Barnsley fern, which leads to 24 numbers all together.

picture 17: Chaos Game with a fern

The fern on the left side is produced by only four affine transformations, which are given in the table below. The figures are taken from the journal “Scientific American”[Jürgens Hartmut, Peitgen Heinz-Otto, Saupe Dietmar: Fraktale - eine neue Sprache für komplexe Strukturen, Spektrum der Wissenschaft (9/1989), p.56.] and the computer-program used is called “Fractal Explorer 1.21”. The picture on the right side shows the zoomed in image of the left lower frond which was then twisted by -52 degrees and which looks similar to the whole.

Starting the chaos game means to choose any point on the plane and using one of the given functions after the other at random with marking all resulting points. Excluding the first points, where the system has to balance itself out first, will lead to the final IFS-picture. This final form, picture, of using the transformation-rules to is called the attractor of the system. For one and the same setup of an IFS there exists only one attractor, which means it will always lead to the same final picture. If we think about the important influence of the planning stage or the process used to develop a design for painting or architecture the IFS underlines the same large effect of starting rules on the resulting end product[04] .

The transformation given above can also be expressed by a polar transformation as follows:

Therefore the new set of equations is:

 and are the scaling factors, and two rotations and “E” and “F” two translations.

Some sets of functions and the correspondent values, e.g. for a fern, can be found in "Scientific American”[05] . Representing the same fern in good quality on a television screen requires defining and fixing over a hundred thousand points. This means that if we find the set of functions, the algorithm, of objects we can reduce their quantity of information - this is important in the case of compressing pictures on the computer. How can we get the set of rules for any picture? We choose certain transformations, by trying out on the screen, and apply them to the original image. If they change the image only a little bit, then the resulting image formed by the transformations will be similar to the original one - we have found the right rules.

Footnotes

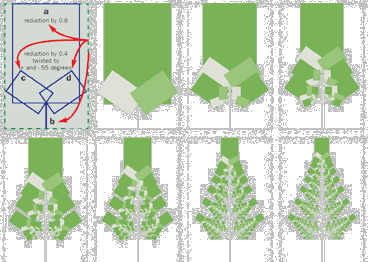
[01] IFS which produce forms that look like real plants work like the copy machine, introduced in picture 02. In this sense they belong to the same category of true mathematical fractals as the Sierpinski Gasket.
[02] Jürgens Hartmut, Peitgen Heinz-Otto, Saupe Dietmar: Fraktale - eine neue Sprache für komplexe Strukturen, Spektrum der Wissenschaft (9/1989), p.54.
[03] The equation for the movement of a point along a line is defined by X(n+1)=AxX(n)+B which leads to different results depending on the chosen values for A and B. E.g. the starting values X(0)=4 and A=-1, B=0 result in X(0)=4, X(1)=--1x4+0=-4, X(2)=-1x-4+0=+4, X(3)=-1x4+0=-4, X(4)=--1x-4+0=+4, and so forth. This means that the transformation jumps between two points: +4 and -4. Changing the strating values to X(0)=+4, A=-0.25, B=1, the results are then turning to: X(0)=+4, X(1)=-0.25X4+1=0, X(2)=-0.25X0+1=+1, X(3)=-0.25X1+1=+0.75, X(4)=-0.25X0.75+1=+0.8125, X(5)=+0.7969, X(6)=+0.8008, X(7)=+0.7998, X(8)=+0.8000 and so forth. As this set of results show, this second transformation is slowly approaching a fixed point around the value of 0.8. This is then called the attractor in the vocabulary of IFS. Finally the transformation that moves a point on a plane is given by two equations because there are two coordinates for each point on the plane. The function then looks as follows f(X, Y)=(X(n+1)=AxX(n)+BxY(n)+E, Y(n+1)=CxX(n)+DxY(n)+F). Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.54.
[04] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.48.
[05] Jürgens Hartmut, Peitgen Heinz-Otto, Saupe Dietmar: Fraktale - eine neue Sprache für komplexe Strukturen, Spektrum der Wissenschaft (9/1989), p.56.