VII Problems with Measuring

The box-counting method is the most frequently used method for calculating the fractal dimension of images and plans throughout this paper - see chapter "4.2.3 Box-Counting Dimension 'Db'". Hence it is necessary to sum up the various problems that may arise by using it - e.g. caused by the dependence of fractal dimension upon the quality and preparation of the image, the sizes of the biggest and smallest boxes used - that is the definition of the upper and lower scale for measurement - and the starting position of the boxes in relation to the image.

7.1 The Size and the Quality of an Image

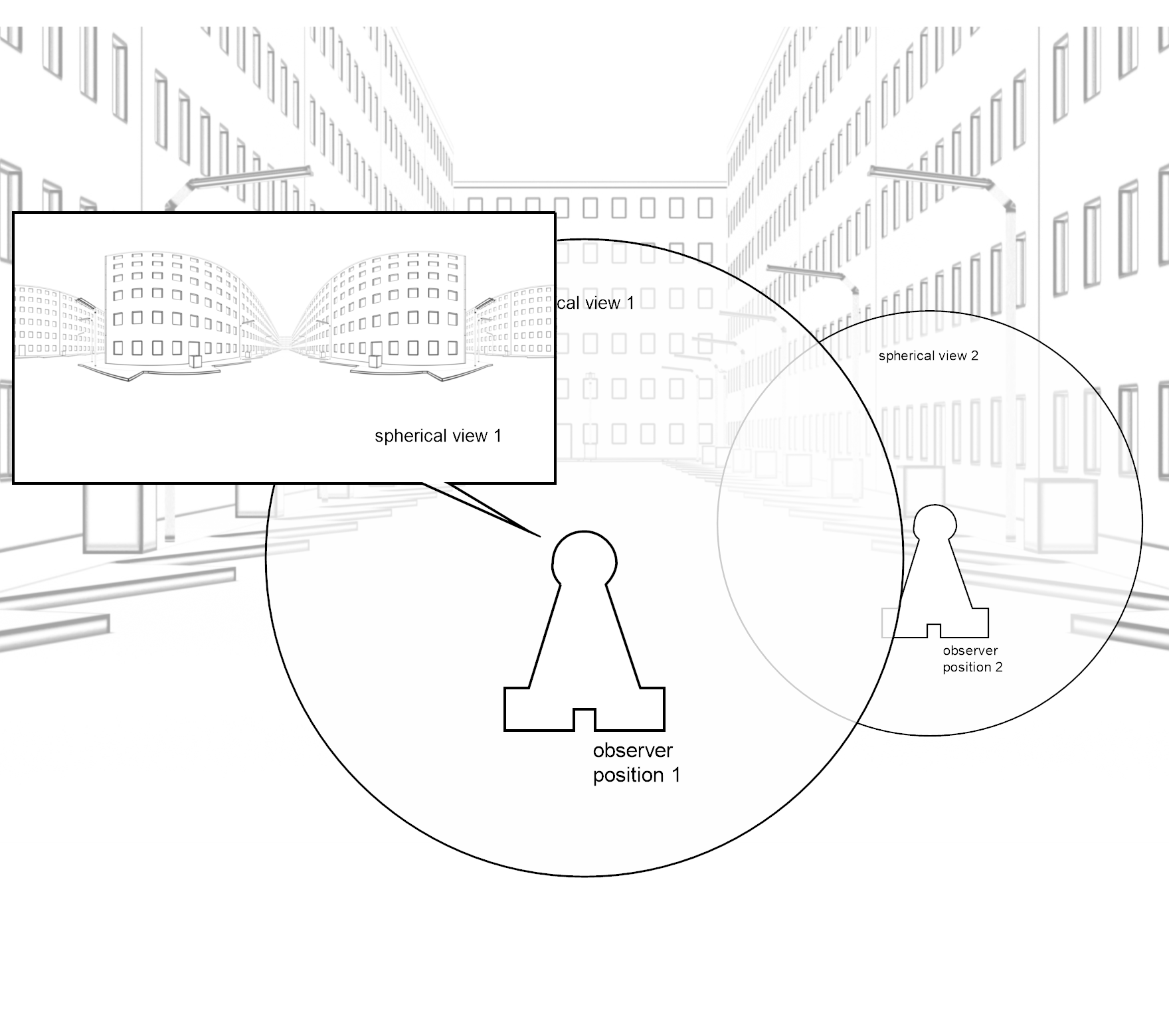
First of all it is necessary to remember that the image or the plan of which the fractal dimension is finally calculated only represents a simplification of the real object, e.g. of the front of a building. In this connection plans of smaller scales generally display more details of the building than those of bigger ones. This is quite similar to the distance of the observer to the real object: if one stands far away, something can be hardly recognized, except one uses a pair of glasses - compare picture 28. Getting closer, which means increasing the scale of the plan, the details become visible - certain details can only be identified from a certain distance or scale on. Thus translating an object into a plan first of all means to define the distance- or the scale-range - with the aid of the biggest and smallest recognizable detail. Using box-sizes beyond this range, in connection with the measurement of the fractal dimension by the box-counting method, this leads to falsified results - no additional details of the real object, the building, are included into the calculation because the plan does not contain them.

Looking at the Koch curve and other mathematical fractals this would mean that, depending upon the distance they are observed from, the number of iterations can be defined. E.g. from far away maybe only the first three iterations will be distinguishable, and all iterations from then on do not seem to change the image any more. Up to a certain scale the calculated box-counting dimension will give some conclusion on the fractal dimension of the real object. But then, if too small boxes are used for measurement, that is the scale-range of observation remains too low, the image will quickly turn out to be a one-dimensional line. From then on no additional details can be picked up because the image does not contain them - the length of this curve is limited in contrast to the real Koch curve.

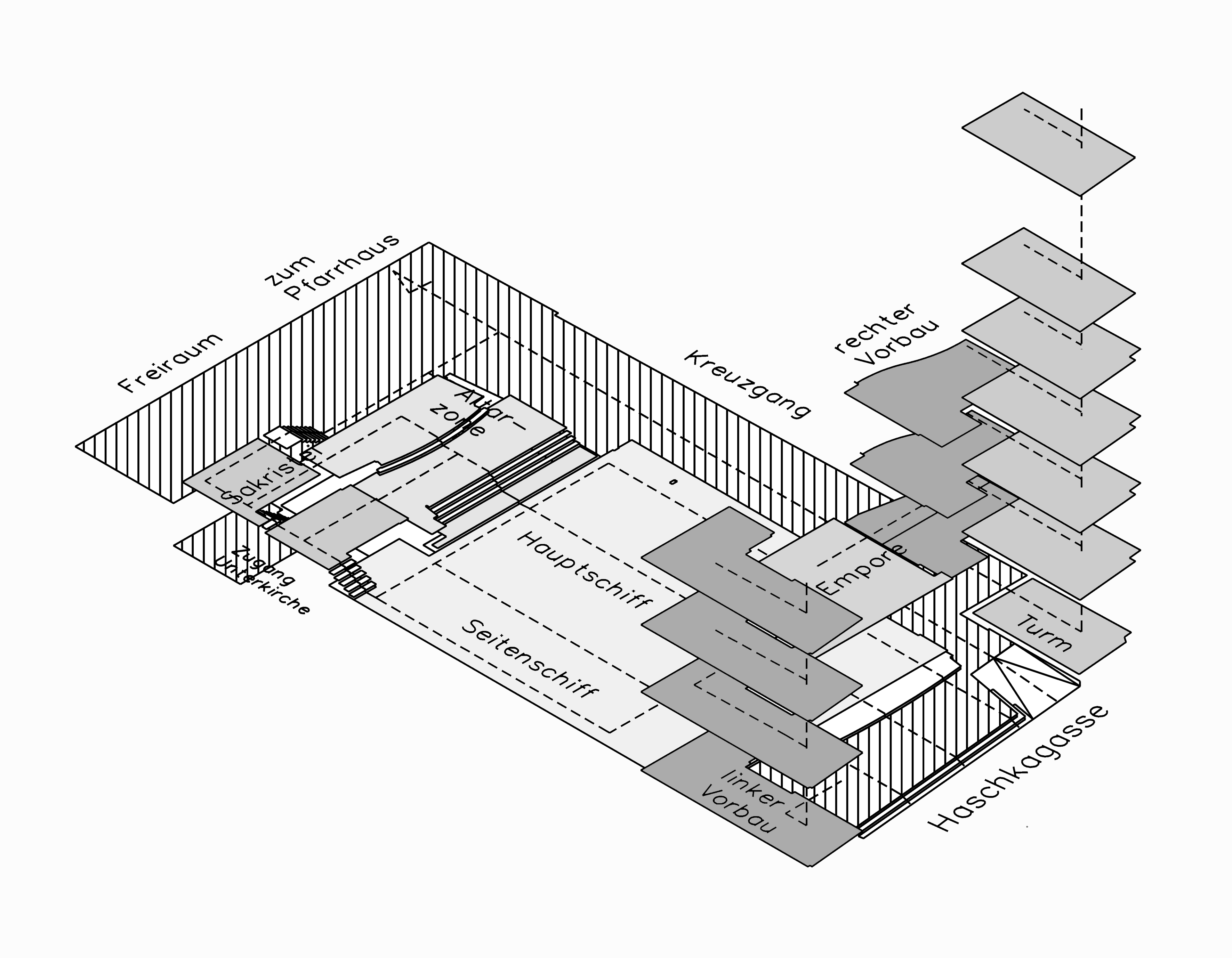
Some other influences represent the quality of the image itself, which may be translated into the language of the computer by the number of pixels per inch - high or low definition. "Quality" also means how many details are getting lost only because of the preparation of the plan - by scanning and after-treatment - and not because of the distance, that is scale. Then the interpretation of the wall of floor plans, whether they are painted black, white or grey, influences the results of the measurement. But also the contents of the plan changes the fractal dimension: elevations may also display the environment - natural or built one -, floor plans may contain tiles on terraces and/or sanitary fixtures and other equipment - some closer look at this theme can be found at picture 81. Such differentiations are taken into consideration when analyzing house types in chapter "9Statistics". In general images that represent elevations and floor plans of buildings have to be similar in the way they pick up details, in their quality and in their scale if they should be compared with each other.

picture 81: Comparison of different starting parameters

The box-counting dimension of ground plans used in the following, taken from "Edoardo Gellner, Alte Bauernhäuser in den Dolomiten" by Edoardo Gellner, are measured with the computer-program "Fractal Dimension Calculator" written by Paul Bourke - these results can be compared with the measurement "by hand", which means that a grid is drawn on the image and the boxes are counted by hand, as presented in pictures 83 and 84. The graph below compares the fractal dimension of six different ground plans with different starting parameters. The graph is divided into two lines, a chain dotted and a broken one, which stands for two different types of plans. The first one contains the fractal dimension of the floor plans for images that are scanned with "300 ppi", which means that they mostly offer the "original", total information. The second type, the broken line, represents the same floor plans but with a definition factor of "72 ppi". As the graph shows, the second line is in general lower than the chain dotted one. Finally the three points indicate the fractal dimension of the ground plans with the walls being painted black.

There are some typical problems when computing the fractal dimensions of ground plans:
1. Definition factor of scanning: With a scanning definition factor of "72 ppi" the image loses very much of its original information. The resulting dimensions are much lower than the measured dimensions of the same house with a scanning definition factor of "300 ppi". In the case of the house-parts in Fornesighe - examples 1 and 5 - and Foppa - example 3 - the fractal dimensions range from 1.08 to 1.15 - broken line, columns 1, 3 and 5 -, while those of a definition factor of "300ppi" range between 1.32 and 1.41 - chain dotted line of the same columns. Looking at the results of the complete ground plans of three farmhouses in Fornesighe - examples 2 and 6 - and Foppa - example4 - the same phenomenon can be identified: the dimensions of the "72 ppi" images range from 1.38 and 1.42 - broken line, columns 2, 4 and 6 -, while those of the "300 ppi"-image can be found between 1.53 and 1.57. If I maintain that a "72 ppi"-image offers less information than a "300 ppi"-image, I proceed from the same total sizes in centimeters with different definition factors.

2. Information: The plans of the house parts in Foppa and Fornesighe offer less information, which means that they are much smoother than the complete plans of the farmhouses. Therefore the fractal dimensions are lower than those of the more complex total plans. Looking at the complete floor plans, example 2 in Fornesighe has the lowest dimension - 1.53 at "300 ppi". The fractal dimension of example 4 in Foppa is 1.56 and that of example 6 in Fornesighe 1.57, which is not much higher. Though the plans are different in their characteristics they offer some similarities: they are not rectangular, they are somehow irregular and they seem to have grown "naturally" - not planned at once -, which is mainly true for the last example.

3. Different qualities: Whether or not the walls are defined as additional information, they remain white or they are painted black. If walls are interpreted as hidden parts of the house, they are excluded from measuring, which means that they are kept white, empty areas: that may be interpreted that way that because of their invisibility they cannot offer additional information. Otherwise they may be seen as important parts of the house and therefore not only the surface is included in measurement, but the whole mass - black, filled walls. In case of room plans there is a greater difference between white and black walls: the walls painted black result in a dimension of 1.40 to 1.47 - the dimensions of the white ones lying between 1.32 to 1.40. But there is less influence on the complete plans, that is because of the complexity of the whole image: "Db" of the 6th example of the "300 ppi"-image = 1.57 and "Db" of "black wall" = 1.59.

a single room of the farmhouse "FO5" in Fornesighe:
Db for "72 ppi"-image=1.08; Db for "300 ppi"-image=1.32; Db for "walls black"-image=1.45

farmhouse "FO5" in Fornesighe:
Db for "72 ppi"-image=1.42; Db for "300 ppi"-image=1.53

a single room of the farmhouse "FZ10" in Foppa:
Db for "72 ppi"-image=1.137; Db for "300 ppi"-image=1.40

farmhouse "FZ10" in Foppa:
Db for "72 ppi"= 1.38; Db for "300 ppi" = 1.56

a single room of the farmhouse "FO6" in Fornesighe:
Db for "72 ppi"-image=1.15; Db for "300 ppi"-image=1.408; Db for "walls black"-image=1.47

farmhouse 4 in Fornesighe "FO6"
Db for "72 ppi"-image=1.42; Db for "300 ppi"-image=1.57; Db for "walls black"-image=1.59

7.2 The Range of Box-Size

The absolute smallest possible box-size that can be used for calculating programs represents one pixel, as a resolution limit of the computer and of the digital image respectively. But in general too small box-sizes would mean that every difference caused by the preparation for the computer is also taken into consideration. In consequence the thickness of a line of the image should represent the absolute lowest limit size for the box-counting method. That means if the scale range we are looking at is between one and two pixels and the line is three pixels wide, the dimension of this line on the lower scale increases approaching two, though a line is one dimensional in Euclidean sense. This and the fact that below this scale no more details can be picked up, are the reason why the lowest box-size should be bigger than the thickness of the lines - see pictures 82.

The box-counting dimension of the border of a square and a rectangle respectively: In this case the examples are the same images and boxes as before, but this time we are only looking at the outlines of the squares and the rectangles. The results show us that this time the dimensions decrease and come close to the value of one. This means that the figure is close to a one-dimensional object. In the Euclidean sense this is true because the outline of a square is a line.

The other extreme, the biggest box-size, can be as large as the image itself. But this extreme can be eliminated, because when counting the number of occupied boxes at this stage, it does not make any difference whether there is only one black pixel or many, the result is always one. Only some stages later, decreasing the box sizes, the difference between one pixel and many will be recognized by a low fractal dimension for the first and a higher one for the latter case. So often the first, biggest, box-sizes are excluded from the measurement.

The box-sizes in between the two extremes, the smallest and largest box-size, should generally decrease by the factor two from scale to scale. So the outer borders of the measurement-grid remains the same, and by that the relative position from one box-size to the previous one.

7.3 Starting Points

There is more than one possible starting-position for the boxes to be laid over the image. E.g. the left bottom corner of the box may be identical with the left bottom corner of the image. But it is also possible to start three pixels left and two pixels down of the corner of the image. In this connection pixels are used because most measurements of this paper were made with the computer and so the lower limit of resolution is one pixel. Thus if the box-size is only one pixel then the starting point has only one possible position on the bottom left side and each box of this grid is exactly one dot of the image. Whereas if the box-size is 2 by 2 pixels, four possible random origins are possible: first all four pixels are situated on the image - the left lower pixel of the box is identical with the left lower pixel of the image -, secondly only one pixel is located on the image - the origin of the box is one pixel below and one left of the image -, thirdly the lower half of the box is outside the image and fourthly the left half sticks out. If the box-sizes increase, there are of course even more possibilities for the position of the starting point of the box - see picture 83.

picture 83: Starting position of the boxes

The relative position of the starting box to the image has some influence on the results of the fractal dimension. The same is true for the size of the first box. On the following two pages I have changed these starting values for two of the previous examples.

A single room of the farmhouse "FO6" in Fornesighe: If the relative position of the boxes and their size do not change, the number of boxes at the basis is not important, that means that the "white" area around the image can be small or big - the results are the same.

farmhouse "FO6" in Fornesighe: In the picture below the position of the building and boxes respectively have changed in relation to the measurement of the "300 ppi"-image, shown at the bottom. In both cases the fractal dimensions from the 3rd stage onwards are nevertheless quite similar.

How do computer-programs manage such problems - see picture 84? E.g. the computer program "Benoit" starts with a defined side-length of the largest box. The user can change this starting size, but usually this is given by one-fourth of the width or height of the image. Beside that he can also define the decreasing coefficient of the box-size. To minimize the error deriving from the box-sizes and starting positions, the program defines a certain increment of grid rotation - the grid rotates with a certain angle. For each grid-position - rotation - the occupied boxes are counted. The computer-program then calculates the minimum number of boxes occupied by the image for each box-size - following from that it does not matter whether the boxes exceed the image or not[01].

picture 84: Measurement programs

For better comparison, it is important to use the same measuring-program, because different programs may lead to different values of fractal dimensions - the differences mainly derive from the starting positions of the boxes. I have measured some of the floor plans of picture 81 by hand and then with the computer program "Benoit" - the results are given in the chart below.

a single room of the farmhouse "FO5" in Fornesighe
"300 ppi"-image; "72 ppi"-image; "black wall"-image

results: farmhouses.pdf

7.4 The Slope of the log-log Graph

The slope of the log(N(s))-log(1/s) graph defines the fractal dimension of the object, which is getting more exact, the more results - N(s) versus 1/s - are available. Points of the graph that are situated beside this slope - line - may indicate that first the image of observation is not a fractal, secondly the box-sizes are defined as too big or too small, thirdly the image-quality is bad or fourthly as mentioned in the previous chapter the image is multifractal. In the analysis of house-types of chapter "9 Statistics" this circumstance is brought in by the position of the points of the graph in relation to the slope: the results are called "very smooth" - the points are congruent with the slope -, "smooth" - indicating minimal deviation -, "diverging" or "strongly diverging". The last two cases are excluded from measurement because it is not clear whether elevations are multifractal or if the deviation results from the influences as described before, like bad quality, wrong preparation and so on.

7.5 Programs

The measurement of the fractal dimension of one and the same image with different computer-programs may lead to different results - if the same image with the same quality and size is run through different programs, this will offer the differences in computing-adjustments. Some of the differences of the programs are given in picture 84 where I have used different computer-programs - "Fractal Dimension Calculator" and "Benoit" - for the same calculations. In comparison and for better understanding I have also measured the box-counting dimensions of some images by hand.
The instruction of the "Fractal Dimension Calculator" by Paul Bourke compares some images of known fractals with the results of the dimensions calculated by his program. Thus the Koch Island has a measured fractal dimension of 1.5, while the box-counting dimension is 1.53 - the difference between these two results is 1.8%. The Koch "Coastline" has a measured fractal dimension of 1.262 and a box-counting dimension of 1.22, the difference being 3.6%. In the first case of the Koch Island the slope and the curve of the points of the log-log graph are quite congruent, while the curve of the Koch "Coastline" differs a little bit from the straight unit-line. For a Euclidean line the measured dimension is 0.994 instead of 1, so there is a deviation of only 0.6%[02].

Footnotes

[01] "Benoit version 1.2" TruSoft Int'l, Inc. - Copyright (C) 1997, 1999; User manual.
[02] http://www.mhri.edu.au/~pdb/fractals/fractdim (15.04.1999); User manual for a mac program.