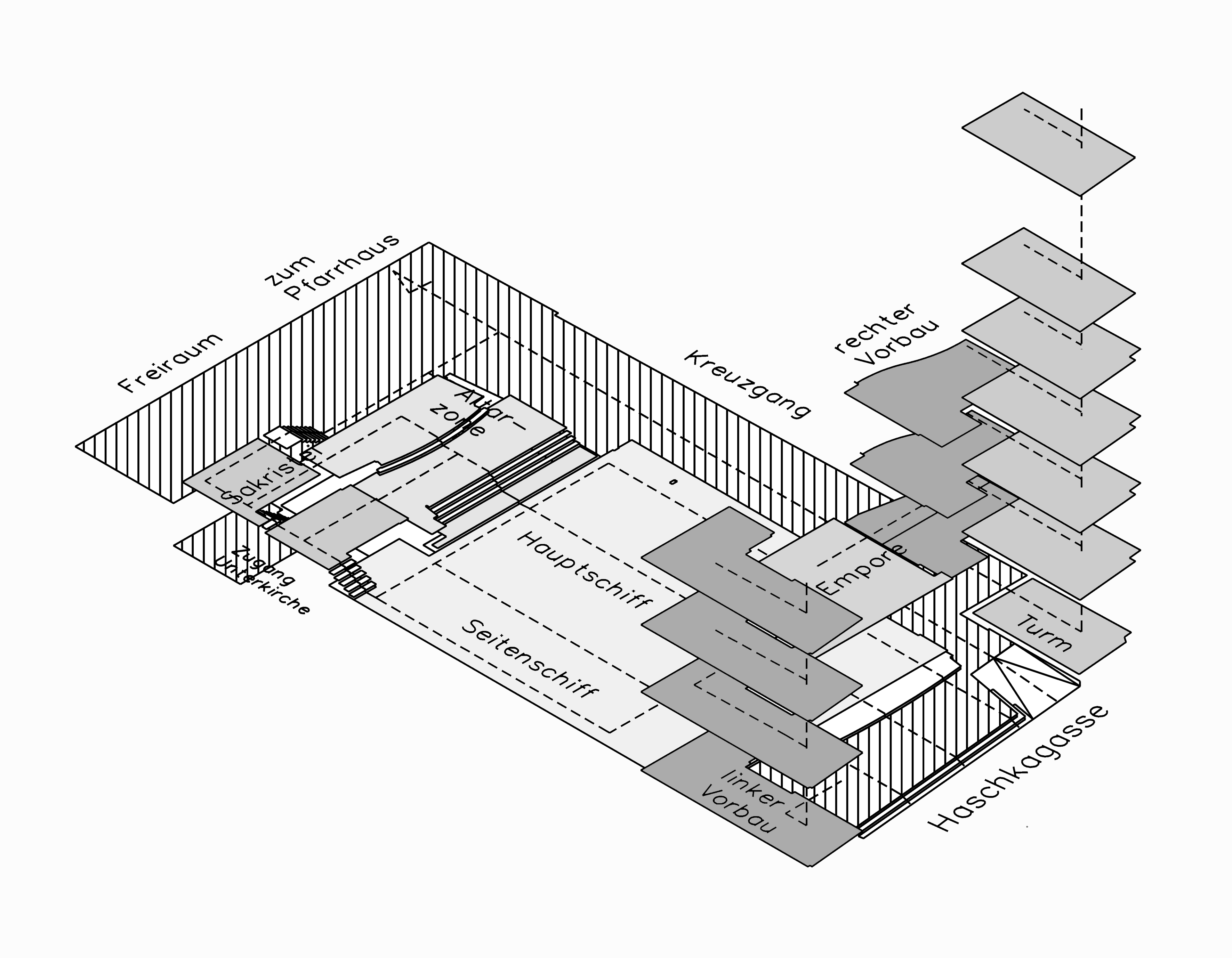
2.2.3 Characteristics - A Fractal is Infinitely Complex

Fractals are highly complex, that means zooming in will bring up more and more details of the object, a characteristic that continues until infinity.

Chaotic fractals: Already in the 20ies of the 20th century the French mathematicians Gaston Julia and Pierre Fatou concerned themselves with the question of fractal geometry. Both examined what would happen to a point “Z” of the complex number-plane if the transformation was repeatedly applied to it[01] . Gaston Julia discovered that calculating the function repeatedly might deliver unforeseen “chaotically” results.

It was only in the 70ies that Mandelbrot[02] could show the results of the formula as a picture, which needed the high capacity of computers. The Mandelbrot set is similar from scale to scale, which means zooming closer to the details there will always come up new parts looking similar to each other and sometimes to the whole - see picture 07. The only limits are limits of capacity and, resulting from this, rounding mistakes by the computer, but also limits of the visual medium.

For further information about Julia sets and the Mandelbrot set see chapter “3.2 Chaotic Fractals”.

Footnotes

[01] Gaston Julia like his rival Pierre Fatou analyzed the phenomenon of feedback. They realized the influence of the constant “C” but they did not have the possibility of computers to generate pictures of its behavior. In simple cases points near the zero point converge to a certain point - fixed-point of f(z) -, while outer points approach infinity. In between those two areas there is an infinitely small border that is today called Julia set. Points of the two areas tend to stay away from this infinitesimal border, to outer or inner areas. Jürgens Hartmut, Peitgen Heinz-Otto, Saupe Dietmar: Fraktale - eine neue Sprache für komplexe Strukturen, Spektrum der Wissenschaft (9/1989), p.59
Gatson Julia wrote his knowledge down as a war-injured person in a military hospital in 1918. Both, Julia and Fatou published their knowledge in mathematical sentences which remained forgotten after their publication in 1918 until Benoit Mandelbrot found them again. Their work had been done by their great imaginative power which is now brought down on the computer screen and thus visible for everyone.
[02] Benoit Mandelbrot was born in Warsaw in 1924. In 1936 he emigrated to Paris where he studied at the Ecole Polytechnique from 1945 to 1947 - 1948 M.S. Aeroscience in Caltech, Pasadena, 1952 Ph.D. in mathematics at the University of Paris, 1958 moved to USA, member of the research department and IBM-fellow in Yorktown Heights in 1974, professor of practical mathematics at Harvard University in 1984. Benoit Mandelbrot has been awarded the F. Barnard-medal of the Columbia-University, a very rare honour, for the development of his fractal geometry of nature. Mandelbrot from the Thomas-J.-Watson-search department of IBM in Yorktown Heights, New York, has brought a new way of thinking into mathematics and natural science by his concept of fractals. This concept was written down in his book “The Fractal Geometry of Nature” published in 1977.