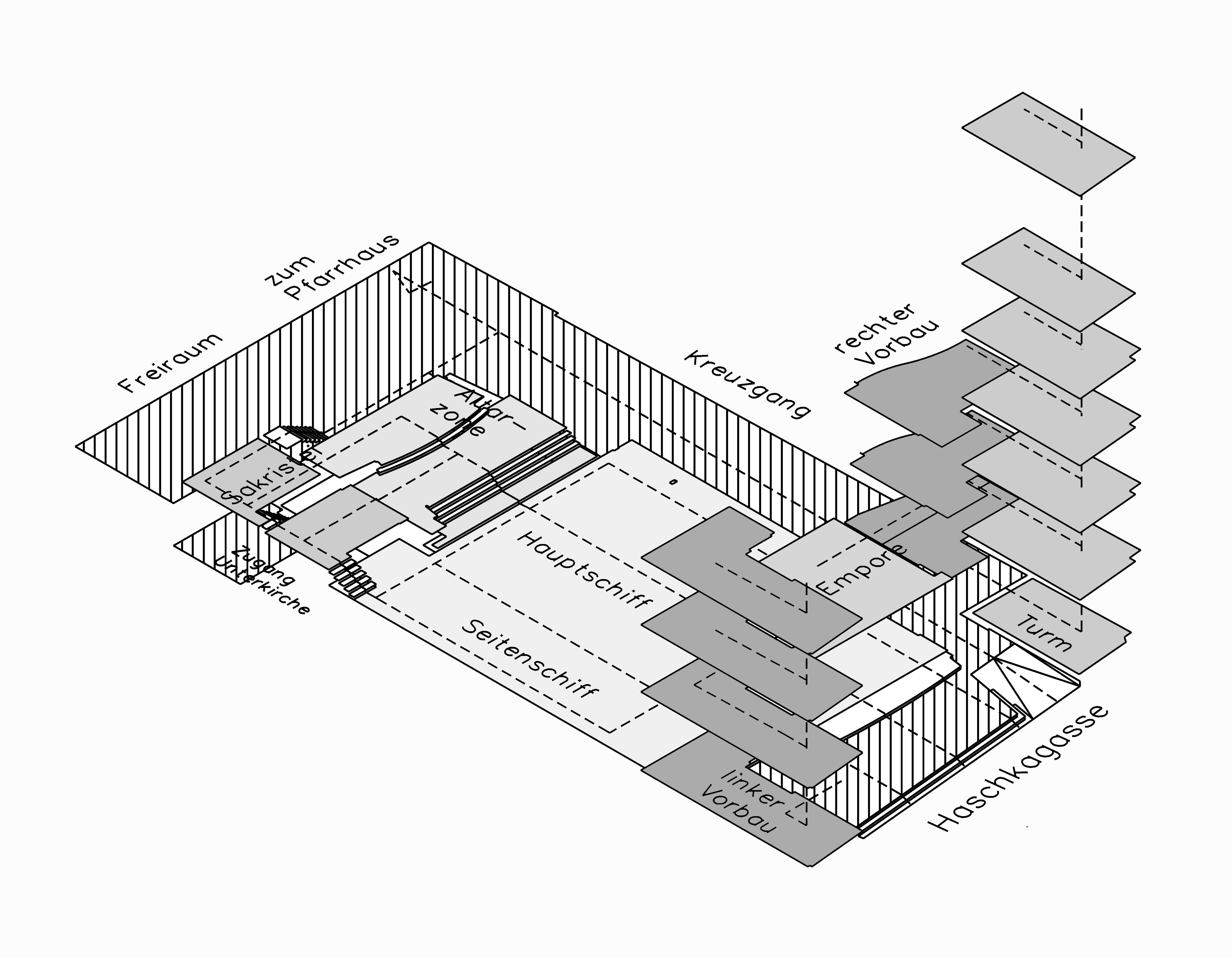
2.2.1 Characteristics - A Fractal is Rugged

2.2.1.a Coastline

Benoit Mandelbrot, the “father” of the popularity of fractals today, introduced fractal geometry by the question of how long the coastline of Britain is. This question of length seems to be very trivial but nevertheless there is more than one possible answer.

To get a better understanding of the problem of length-measurement first of all let’s have a closer look on how the coastline of Britain may be measured: for measuring the length of the outline it is possible to use a certain map with a certain scale, following the coast by a ruler. When we repeat this way of measuring on another map of a smaller scale, the outline turns out to be longer. The reason lies in the fact that the latter map will offer more details, that is sub-bays, inlets, cliffs and rocks, whose circumferences are included in the measurement which finally leads to the increased length, see picture 01. So the coastline may be longer or shorter, depending on the scale of the map we are using for measurement.

Looking down on the coastline from a great distance, out of an airplane, we will recognize the character of the border on principle - if its rough or smooth -, but we will not see all the small inlets which will come up when we are closer to the coastline, for example when walking along the beach.

Nevertheless there are some limits to this length-measurement. One limit is the size of an atom as a physical border - theoretically, without any limit, the length of the coastline would reach infinity at an infinite small scale because of the infinite number of inlets. The other limit is the correct definition of the coastline, that is where the exact border between water and land is and at which time it should be measured, at high tide or low tide. Consequently, it may then be better to choose a rock of about 20 meters length as the lower limit instead of an atom. This value also arises from the fact that regions of coastlines have been cultivated by man -this has turned them into smoother parts. Therefore, to avoid falsifications, smaller scales have to be excluded from measurement.

2.2.1.b Border

Another example of scale-dependence is the length-measurements of borders between countries. The problem of measuring them has been known for a long time and in most cases the deviations do no harm: e.g. the circumstance that the length of the border between Spain and Portugal is given differently by the officials of these two countries has no consequences. The difference results from the fact that the official maps of Spain have a bigger scale than those of Portugal[01] . Here we find the same phenomenon as with the coastline above - the maps of Portugal show more edges and corners, which mean that the border is longer than on the maps of Spain. The length given in the Spanish encyclopedia is 987km and that in the Portuguese one is 1.214 km[02].

Boundaries of cities are similar to borderlines of countries and outlines of coasts - e.g. the political border, the changeover from the city to the natural environment, from high-density built-up areas to low-density areas, from regions of dwelling houses to regions of one-family houses. Nevertheless, there are again limits as with the coastlines above - like the definition of the border, that is defining its way and the limit by the smallest and largest scale. In addition to that the fact that various measuring methods lead to different results is valid for all measurements of fractal dimensions, which will be described in chapter “4.2 Fractal Dimension”.

2.2.1.c Richardson

As early as in the year 1961, Lewis Fry Richardson examined the growth rate of the length for different curves such as coastlines and borderlines, by replacing the original curve by a polygon consisting of equal-sized lines - the unit length. For each curve and for a certain he got an overall length through the approximation formula .
That means that Richardson put the total length in relation to the unit length by using two constants and “D”: “D” depending on the coastline and its roughness.

For comparison, he then decreased the unit length for each curve and measured once more, which led to another greater length , and so on. The results of measurement were put into a graph of log(unit length) across log(overall length)[03] . The curves of each measured borderline of the graph led to a certain gradient angle, which was interpreted by Mandelbrot as amounting to about “1-D”: Mandelbrot called “D” the fractal dimension of the curve, e.g. for a circle the gradient angle turns to zero which equals D=1. 

unit length 300; unit length 100; unit length 25

As unit-lengths lead to different total-lengths, borders, coastlines and other fractal curves cannot be compared by their length. Firstly, because one "unit-length" for all measurements would have to be defined, which has not been done yet, and secondly, nature also exists without man, which means that a typical man-defined unit-length would place man above nature[04]. Therefore the fractal dimension “D” will be a better parameter for comparison.

2.2.1.d Architecture

Facades often display some kind of roughness - for example let’s think of window-frames, the distribution of windows and doors, the character of bricks and other materials, the structure of the roof and the wall.

Footnotes

[01] Spain is a larger country than Portugal, which means it would need more maps of the same measuring scale as Portugal to show the whole country. Voß Herbert, Chaos und Fraktale - selbst programmieren (1994), Franzis-Verlag GmbH Österreich, ISBN 3-7723-7003-9, p.13.
[02] Mandelbrot Benoit B., Dr. Zähle Ulrich (editor of the german edition), Die fraktale Geometrie der Natur (1991) einmalige Sonderausgabe, Birkhäuser Verlag Berlin, ISBN 3-7643-2646-8, p.39.
Another example for a different border-length is that of the Netherlands and Belgium, where the differences in length, given in the lexica of these neighboring countries differ by about 20%. This results from a different choice of unit-length, which means that the smaller country measures its border more carefully on maps of a smaller scale.
[03] Mandelbrot Benoit B., Dr. Zähle Ulrich (editor of the german edition), Die fraktale Geometrie der Natur (1991) einmalige Sonderausgabe, Birkhäuser Verlag Berlin, ISBN 3-7643-2646-8, p.40-41.
[04] Mandelbrot Benoit B., Dr. Zähle Ulrich (editor of the german edition), Die fraktale Geometrie der Natur (1991) einmalige Sonderausgabe, Birkhäuser Verlag Berlin, ISBN 3-7643-2646-8, p.39.