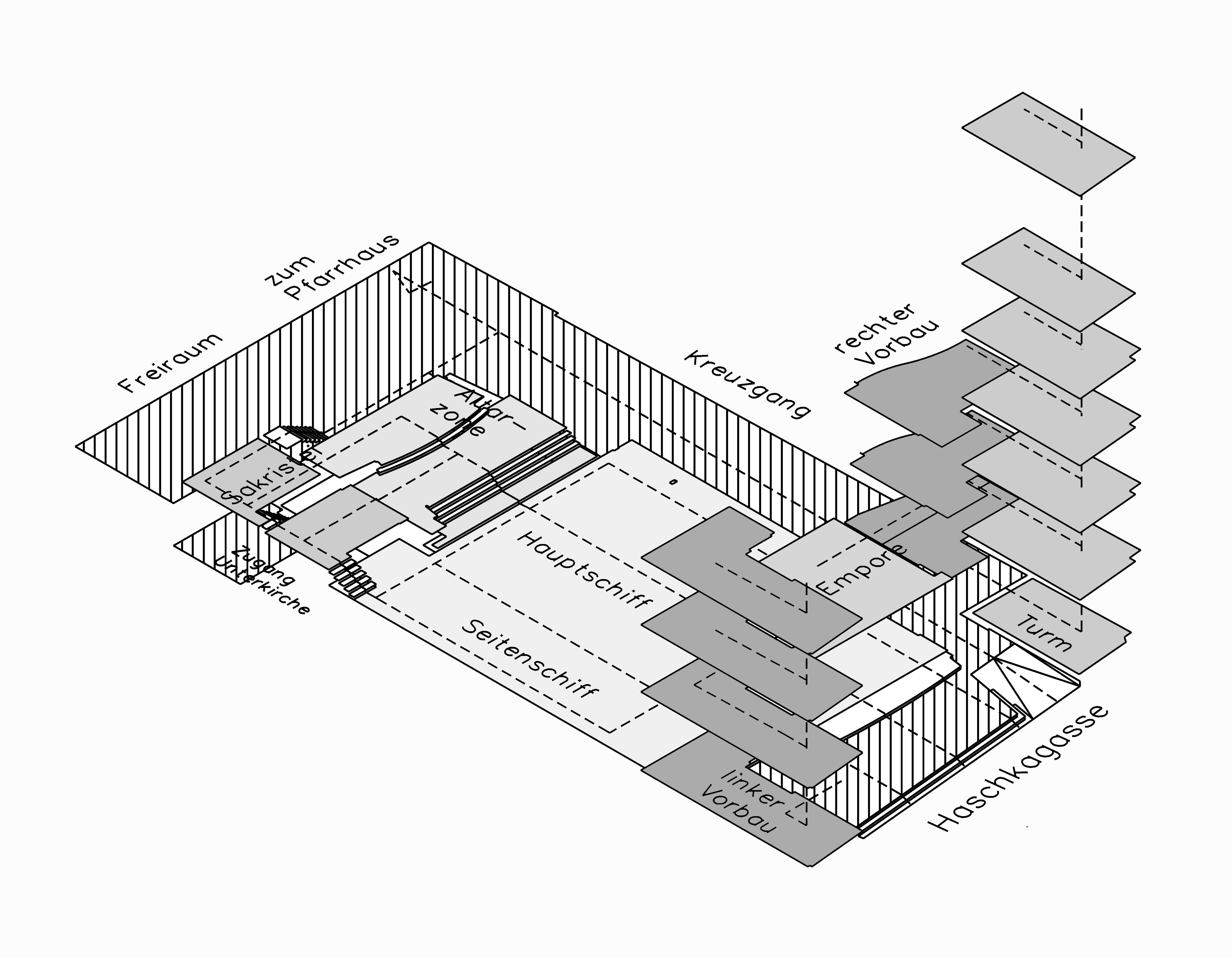
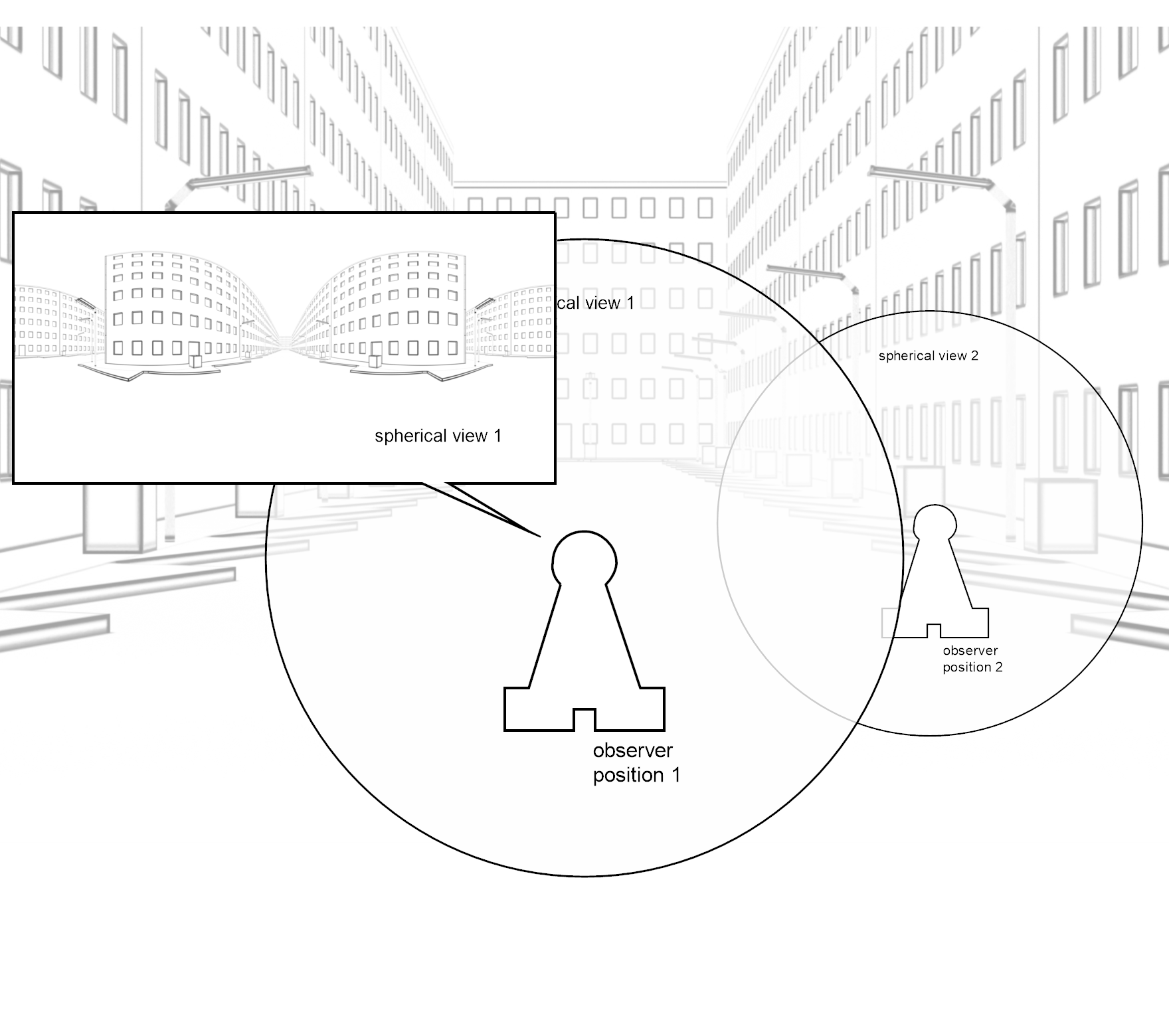
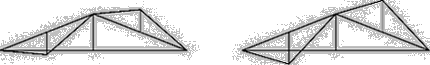Footnotes
[01] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.76.
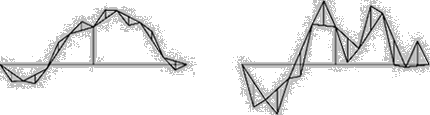
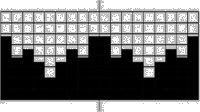
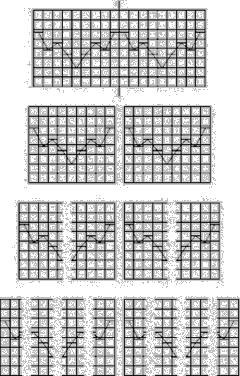
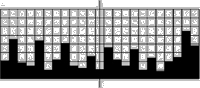
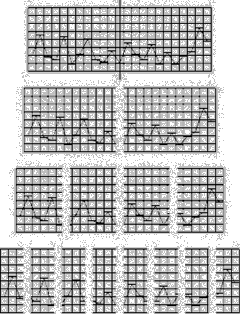
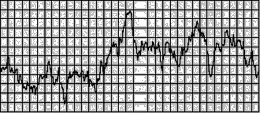
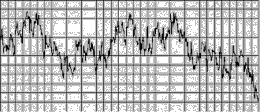
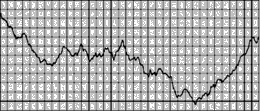
[02] The fluctuations of the fractal curve are statistically self-similar, which means that one part of the curve is not an exact copy of other parts but they are statistically similar. To show this similarity one can zoom in on the curve, but if the vertical and horizontal scaling factor is equal to one, then the resulting curve will be rougher than the original curve. If a horizontal scaling factor of two is choosen instead, the curve will flatten out. Instead of that a properly rescaling can be reached by changing the rescaling factor for the horizontal direction to the value of two and for the vertical direction to the result of 2H. Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.81/82.
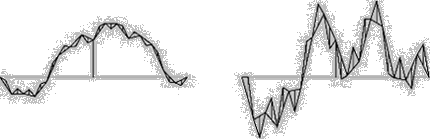
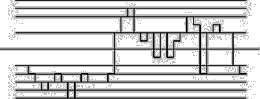
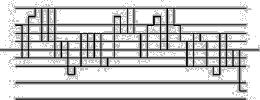
[03] This time it does not matter if the horizontal axis is streched or not because the vertical fluctuations stay the same with the grid. Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.82-87.
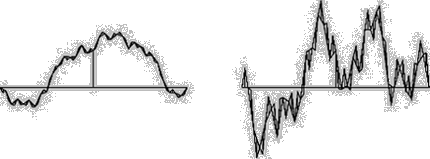
[04] The algorithms of computer programs that generate fractal noise curves are approximations in their simulations which lead to the fact that generated curves with a dimension above 1.5 will result in a little bit lower measured dimensions, respectively curves generated to have fractal dimensions below 1.5 will offer higher measured dimensions. Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.88.
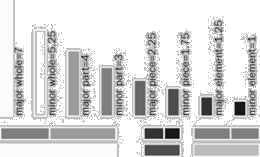
[05] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.167-169.
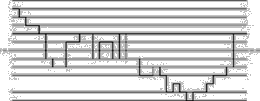
On the one hand too much order does not bring up any surprise, which leads to the fact that the following parts are known, that is determined, from the very beginning - music or architecture is then regarded as boring. On the other hand too much surprise destroys any direction, its parts can be put together in any way, there is not any sequence at all - man is upset and loses any kind of possible orientation.
[06] Fuhrmann Peter, Bauplanung und Bauentwurf: Grundlagen und Methoden der Gebäudelehre (1998), W. Kohlhammer GmbH Stuttgart, p.13.
[07] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.91.
[08] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.158-164.
[09] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.174.