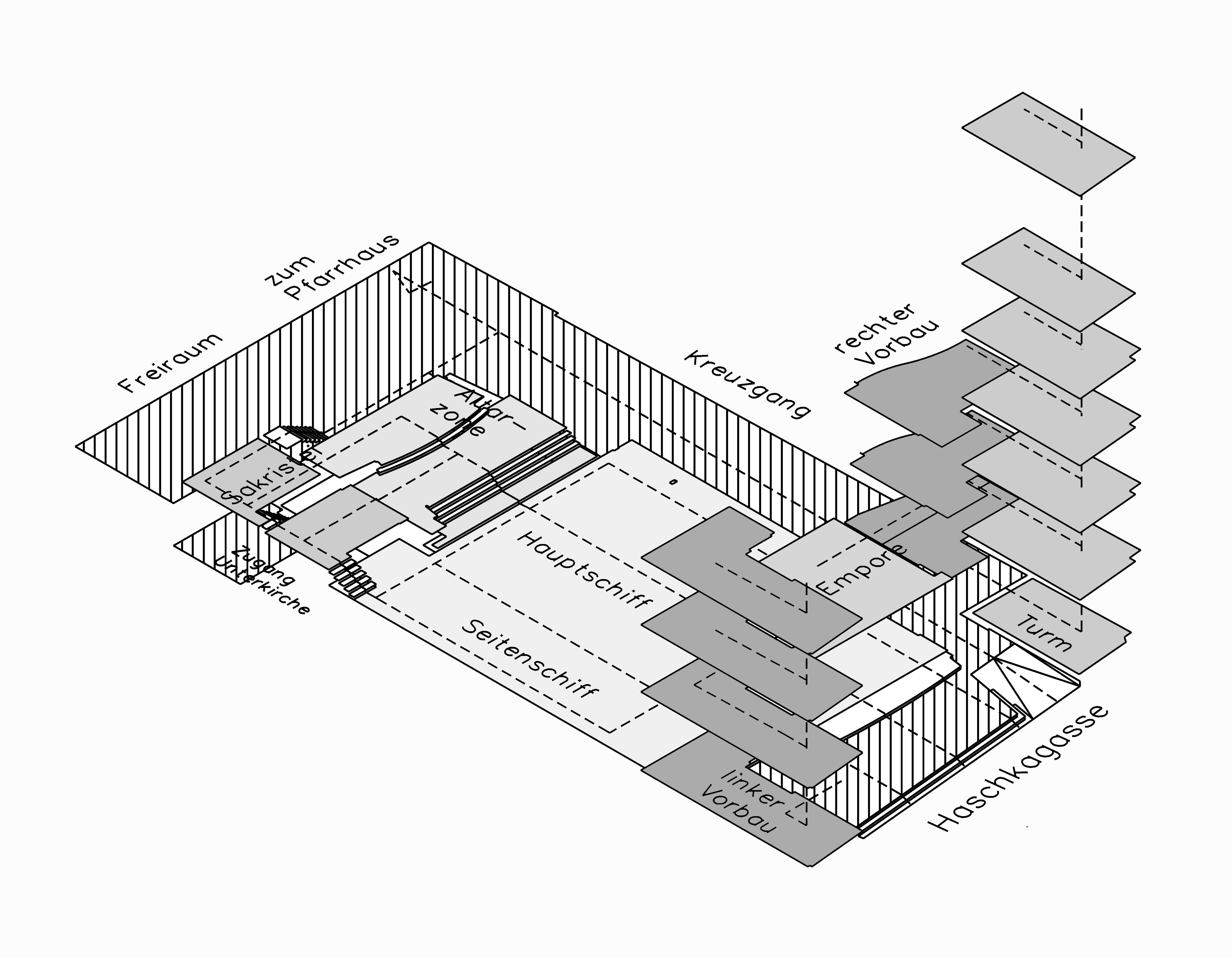
Indigenous buildings generally have a deeper scaling than modern houses. That means that coming closer to the surface, there will always be some new smaller interesting details, similar to the concept of the houses by Frank Lloyd Wright. The different kinds of rural houses depend on the specific region, the available materials, the size, the usage and inhabitants of the building.
In the comparison of two houses taken from "Alte Bauernhäuser in den Dolomiten"[01], one native-house in Gosaldo and one in Borca, the differences of the two regions are visualized. The elevation - the plan of the facade - of the house in Gosaldo seems to be smoother, which is pointed out by the box-counting dimension of the smaller scales:
D(10-20)=(log105-log42)/(log20-log10)=1.322 for Gosaldo
D(10-20)=(log208-log66)/(log20-log10)=1.656 for Borca
The more one zooms into the plan, the lower the dimension will be, which also means that the elevation then offers less additional information and fewer details respectively - the facade does not seem to be very rugged. The elevation of the house in Borca on the contrary offers more and more details the smaller the scale becomes. This is again shown in the fractal dimensions of the surface:
D(20-40)=(log283-log105)/(log40-log20)=1.430 for Gosaldo
D(20-40)=(log688-log208)/(log40-log20)=1.726 for Borca
In the case of Borca the dimension increases from the scale-range of 10boxes to 20boxes to the scale-range of 20boxes to 40boxes, in the example of Gosaldo it decreases. Comparing the dimensions of the plans of both facades on the same scale shows the difference in the overall view, the elevation of Borca has a box-counting dimension of e.g. D(40-80)=1.702, the one of Gosaldo D(40-80)=1.461. This is caused by the different structure of the elevations: the one of Gosaldo offers a smooth symmetrical front-facade with one balcony, symmetrically arranged windows and a small additional section on the left side. The front-elevation of Borca consists of an outdoor staircase, some balconies with wooden carved banisters, asymmetrically arranged windows, timberwork on the gable, a bigger additional part on the back left side and some parts have different heights. That points out that the box-counting dimension indicates the roughness and differentiation of the whole building - the plan respectively. The more rugged the elevation - picture of the facade - is the higher the dimension will be. Besides one can observe the decrease or increase in information when zooming closer, see picture 53.