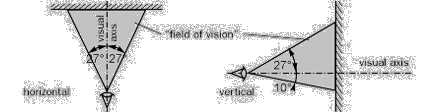
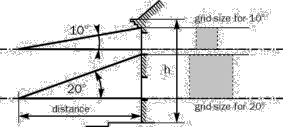
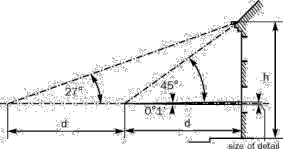
5.1.1 Changing of Dimensions

Benoit Mandelbrot used a wool-skein to show the changing of mathematical constancy - the changing of the "effective" dimensions. For a viewer who is far enough away from the wool-skein, which may have a diameter of 10 centimeters and consists of a 1-millimeter yarn, it looks like a point, a zero-dimensional object. In a 10 centimeter resolution the skein is a three-dimensional object, in a 10 millimeter resolution it turns out to be a confusion of one-dimensional twines, at a 0.1 millimeter resolution each twine is experienced as a three-dimensional column and at a 0.01 millimeter resolution each column turns again into one-dimensional fibers. If we zoom in deeper on the resolution of an atom, the wool-skein is presented as an object of finite numbers of atom-like points and therefore it is again zero-dimensional - remember the Cantor Set. So the wool-skein shows a sequence of different effective dimensions. Some badly defined change-over between zones of well defined dimensions are interpreted as fractal zones where the fractal dimension is higher than the topological one[01].

Benoit Mandelbrot also wrote about the surface of timber being spongy but nevertheless the beam is said to be even. This is because of the scale, in a certain ratio of size the regular and continual aspect can describe an object in a correct way. He compared this scale with a tinfoil that is put over a sponge, which follows the surface but does not show the many little complex details, see picture 26[02].

5.1.2 The Scale-Range of a Wall

Observing a straight wall, built of stones of a certain thickness, height and length from a great distance, the object may look like a straight line - e.g. having a look at the Great Wall of China from the universe it will be identified as a long curve with no width and no height. But coming closer the curve turns into a two-dimensional plate with a certain height and length but no width. Finally standing on the wall it will turn out to be a three-dimensional object. Then looking at a small stone as part of the wall a couple of meters away, this stone may be experienced as a zero-dimensional point. But coming closer once more, this stone turns into a three-dimensional object. This changing of dimension can be repeated down to the scale of the atom, which offers a physical border, see picture 27.

picture 27: Great Wall

5.1.3 The Scale-Range of an Elevation

The changing of the "effective" dimension is also true for other man made objects. E.g. observing a building from far away it may seem to be a point or, thinking of rows of houses, maybe a line. Coming closer the two-dimensional outline can be recognized but no deepness of the elevation. Windows seem to be points and lines. When analyzing the elevation from the front it cannot even be said if it is only a stage-prop. Coming closer up to a couple of meters away from the building, more and more details like cuts of the windows and the jumping forward and back of elements of the facade come to one’s attention. On this scale the house is experienced as a three-dimensional object. At some point even the roughness and structure of the facade can be felt; it, however, depends on the material of the surface of the building at which distance this will be. In front of the door some more details like the doorknob can be found, which may have looked like a straight line before[03].

Using Euclidean vocabulary implies a certain abstraction such as a plastering facade is actually rugged but is mostly called smooth. This abstraction is taken from a certain scale, a certain measuring: the man and the human body. From a certain distance the facade really looks like the Euclidean flat plane, though thinking of a brick wall, there is always a structure to be observed. This leads to the conclusion that the cut out windows and doors, beside other details such as the structures of walls and door knobs, are what the facade differ from Euclidean shapes at this scale, which is also true for smooth concrete facades. Therefore the straight smooth modern style buildings are also fractal forms on closer observation.

At the next stage, when entering the house, the next level of the object is examined. There is a difference between smooth rectangular buildings and a building of differentiated ground plans and elevations. It is easy to take up the first type at once and explain its rooms with a few words. In contrast to that, a “differentiated” house with different heights, different materials has more underlying information to offer. But if there is too much that we cannot understand in the context this can lead to an oversupply of information like in a language we do not understand. In this case the complexity turns into confusion.

5.1.4 Conclusion

“Architectural composition is concerned with the progression of interesting forms from the distant view of the facade to the intimate detail. This progression is necessary to maintain interest”.[04] 

The principle of stepping forward of details by zooming, which is mostly found in nature, should be taken up as a reflection of the intention of the composition from the whole to the detail. This means that for example a round surface asks for round floor plans, which also means that the resulting concept is understandable from the whole to the detail.
This is the fractal concept: self-similarity from scale to scale, but of course in a more general view as with true mathematical fractals. By that, each distance, scale offers a certain attention to details. Fractal structure therefore stands for the continuing of an architectural composition from distance, the outer elevation, the interesting detail from outside to inside and the shaping of the interior, which means entering and “using” the respective scale[05].

The scaling range of an object, and depending on that the grid-size for the box-counting method, is related to the nature of visual perception. Very fine details can be observed only within a range of two degrees from the center of the inspected object. But significant details are also realized from an angle of 10, 15 and 20 degrees - see picture 28. Each scale has a certain distance to the observed object, which can be expressed by the equation: the distance from the building multiplied by tangent of the angle is equal to the measuring unit size. But there is a difference whether one concentrates on a certain detail or on the whole from the same distance. In the first case, looking at the detail, e.g. a short line in an abstract painting or the doorknob of the entrance, objects around it will also come to our attention. If we concentrate on a larger detail or the whole, e.g. the elevation of the building, smaller details run out of perception[06].

2. "Region of very sharp perception": The picture below shows a diagram of the location of rod and cone cells in the human eye, taken from "Fractal Geometry in Architecture and Design" by Carl Bovill.[09] Details are perceived in the middle part, the fovea and macula. While fine details are only observable within 2 degrees - i.e. a sight cone with an opening angle of 1° -, significant details can also be observed through 10, 15 and 20 degrees.

Footnotes

[01] Mandelbrot Benoit B., Dr. Zähle Ulrich (editor of the German edition), Die fraktale Geometrie der Natur (1991) einmalige Sonderausgabe, Birkhäuser Verlag Berlin, ISBN 3-7643-2646-8, p.29.
[02] Mandelbrot Benoit B., Dr. Zähle Ulrich (editor of the German edition), Die fraktale Geometrie der Natur (1991) einmalige Sonderausgabe, Birkhäuser Verlag Berlin, ISBN 3-7643-2646-8, p.20.
[03] The elevation informs us about material, in some respect of what happens inside - staircase, kitchen, office -, the lightness of the rooms - through windows -, maybe about construction, forms, functions, but always in connection with knowledge of similar types, materials, forms and logical relations.
[04] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.5.
[05] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.118-119.
[06] Bovill Carl, Fractal Geometry in Architecture and Design (1996), Birkhäuser Bosten, ISBN 3-7643-3795-8, p.118-119.