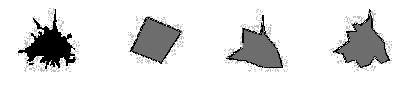6.2.3 Naturally Grown Cities

The simplified growth model of the "organic" city spreads out from one center of initial growth or seed in form of waves of development. This first approach can be modified by radial lines of transportation along which growth often proceeds faster - resulting in star-like shapes -, but also by the shape of terrain - rivers, hills and the like - and possibly existing defensive walls - restriction of growth, see picture 72[01].

picture 72: Growing models

radial and star-like - and defensive wall of Vienna as a restriction.

For developing more realistic models, patterns of real cities have to be taken into consideration with respect to their growing through time. But if such a development of cities - visual history - is analyzed with regard to some deeper order, several problems will arise: e.g. the different quality, detail richness, scale and exactness of the presentation of city-plans, which have been changed during the centuries and the absence of unbroken availability of maps make statements more difficult. Beside that, most cities before modern age were small and compact with higher density caused by slower transport and range. This changed with better and faster transport-systems and building technologies - since the 17th century the city walls have gone and the industrial era began -, which led to bigger cities with lower density[02].

Another aspect that should be taken into consideration is that "irregular" - "naturally" grown - and "regular" - "planned" - forms vary within the same city with respect to scale - at one scale the city may belong to the first, on another scale to the second group. That means, if the shape of the city can be defined through its fractal dimension, then this dimension will change through scale - see picture 73.

picture 73: Scale

"irregular" and "regular" forms vary with respect to scale - plan of Vienna.

6.2.3.a Form, Structure and Hierarchies

"Form is the shape of contents"[03]. From this follows that with respect to cities, first - in the sense that the word "form" refers to the shape, the outward appearance - form represents the spatial patterns of the physical elements that cities consist of. These elements belong to the following three categories: 'networks' - e.g. transportation networks for people, goods, water, energy and information -, 'buildings' - including residential, commercial and industrial buildings -, and 'open space' - such as parks, gardens, places and courtyards. But, secondly, the word "form" also involves the forces that create this visual shape, and with regard to that it is important with the study of form to think about the processes which give rise to it. The first association of process with form is that of 'growth' - the dynamic viewpoint -, involving the changing of objects through the interactions of forces - "organic form". The second association is 'function' in the sense that processes, containing the forces that produce form, have specific functions - hence form is understood as the product of functions[04].

Hierarchies: As following from above, the external form - the shape - can be described by its internal, invisible form - the structure. The structure is itself composed of elements, so-called basic components, and their relations, the interactions and functions of elements. With respect to cities the elements are called units of development - the housing or a 'block' -, which are linked to each other through various communication networks. The related functions of the elements belong to employment, commerce, education and recreation. All these elements and relations - structure - of cities cause their complex geometry - shape[05]. In general, decomposing the system structure, producing subsystems, involving sets of components which can be arranged according to a hierarchy, in which the subsystems and the elements respectively, may reflect the same form at different levels: self-similarity - see picture 74[06].

Cities are organized hierarchically into neighborhoods whose rank and the spatial extent depend upon the economic function which they offer to the surrounding population - specialized centers serve larger areas, whereas those of local needs serve smaller ones. This hierarchy in cities is formed by centers and their hinterlands, which have several elements - functions - in common, starting with the Central Business District - CBD -, followed by some district centers, a larger number of neighborhood centers and even more local centers[07]. Such a hierarchy also exists for the transport system - reaching from primary or trunk down to local distributors, from freeways to pathways - the educational and the leisure system.

Just the other way round, the self-similarity on different scales, such as represented by the centers within cities, can be generated if one knows the right functions and rules respectively. These rules - involving office, government, trade and commercial functions, the range and multiplicity of goods and services and the quantity of population served - are then applied recursively on every scale, starting with the largest center, the CBD, leading to different ranks in the hierarchy of centers[08].

Classification: The idea of self-similarity and hierarchy can also be carried on by comparing the classification of rooms in a dwelling with the classification of parts of the city. On such different scales, there are always sections for leisure, traffic, working and living: e.g. from the freeway over a footpath to the corridor of the dwelling, from the entrance of the city to the entrance of a building, from the office-tower to the desk, from the big supermarket over a smaller food store to the refrigerator.

6.2.3.b Growth Models

The DLA model, introduced in chapter "3.4 DLA Models - Diffusion-Limited Aggregation Model", can be treated as a baseline model for simulating the growth of cities. The spatial patterns of cities evolve, similar to the DLA model, by adding cells or basic units - individuals, households or transportation links, represented by their occupied space - around some central point - the CBD. This leads to tree-like or dendritic forms, which show fractal characteristics such as self-similarity - see picture 75. Batty and Longley mention in their book "Fractal Cities" that the growth process itself contains codes which determine how the organization of the basic units might display the self-similarity of forms and functions. That means if the growth of cities is planned at any scale, the individuals or agencies involved almost subconsciously take account of economies of agglomeration, the requirement that the surrounding population is served efficiently by similar functions and services of different order on different scales, linked by transportation systems - this minimizing costs and effort[09].

picture 75: DLA-simulation and a "real" city, Cardiff

dendritic growth based on a 500X500 lattice and the urban area of Cardiff

When looking more closely at the growth process of the DLA model and that of cities some differences appear. First, the structures produced by the DLA model grow irreversibly in contrast to urban development, where the individuals are free to move, hence it is possible that already occupied cells become again unoccupied; secondly, the patterns of cities are more compact; thirdly the random walk of the cells of the DLA model - before they are fixed - has no analogy in cities. Beside that, to get a comparable dynamic structure of real cities in respect to the DLA model, the position of each individual and its related space respectively has to be known at every time. In the absence of proper data the structure of real cities can be simplified by dividing the city into a grid - with a lateral length of e.g. 50X50m -, getting the distribution of the population by census. The "occupied" fields of the grid are then treated like the "living" cells of the lattice of the DLA model. This of course leads to a more general and coarse image of the city and offers less dendritic forms. Anyway, with the aid of distance and the density or the number of occupied cells respectively, the fractal dimension of the city can be measured.

The Dielectric Breakdown Model - DBM - offers a more realistic growth model, dealing with the relation between fractal dimension and compactness. Compactness can be changed through a certain parameter - lowering the probability of occupying a cell can increase the compactness[10]. Moreover natural restrictions can be brought into diffusion by the factor of unlikely or forbidden development in certain areas - e.g. in the case of mountains. Beside that the development of additional models may produce tunnels or bridges - see picture 76.

picture 76: DBM-simulation

dendritic growth based on a 150X150 lattice

the simulation of the urban growth of Cardiff using the Dielectric Breakdown Model (DBM) - the river and harbour being restrictions of the system.
h is the control parameter, used in an equation that determines the probabilities of sites being selected for growth on the boundary of the cluster. As h increases the average dimension falls and the form becomes linear.

6.2.3.c Urban Boundaries

In general, boundaries are dividing and connecting at the same time, marking the transition between different uses or territories. From this follows, that urban boundaries can be defined as the change-over from the urban to the rural area, e.g. indicated through different land-uses that reach from high density commercial uses at the CBD to low density agricultural uses at the edge of the city including differences in their built-up density - villages that are connected to the urban area by some development may also be related to the city. Beside the definition through land uses, the population density also gives information about where the separation of the "city" from its environment takes place - from high density or urban to low density or rural area[11]. It is obvious that the course of the urban boundary ultimately depends upon the definition of the changeover, that is which kind of land-use is included and what the limiting value of population density is respectively.

Anyway the resulting lines look irregular, not smooth in form and are closed, marking out some area, from which follows, that urban boundaries are more than a one-dimensional - straight - line and less than the area it encloses - it does not fill the entire plane. Thus the fractal dimension may be between 1 and 2, the final value depending upon what is measured - which is the final definition of the course of the boundary - and which method of measuring is used - e.g. different results through the structured walk method and the cell count method -, see picture 77.

Their fractal dimension can compare the boundaries of cities with each other, like Richardson had done with coastlines and borders of countries - see chapter "2.2.1.c Richardson". But what are the reasons for the different degree of irregularity at the edge, and resulting from that for the different fractal dimensions of city boundaries[12]? First, their form and shape is determined by physical constraints presented by the specific geography of the area, including steep terrain, the sea and lakes, the course of rivers, which themselves have often been changed by man - straightening leads to lower fractal dimensions -, and generally areas that can hardly be built-up - including the dependence upon the conditions of the soil. Secondly they are influenced by the improvement of building and transportation technology, which are both connected with the history of the city. Thus the development of the tramway enabled a better accessibility of the area of the city and the introduction of concrete and the assembling construction in prefabricated units respectively gave way to cheaper and faster building and by that to more spacious suburban housing - both lowering the fractal dimension of the edge. Thirdly patterns of land tenure, the size of building plots and the demand for residential space also represent possible influences[13].

In any case, cities can be observed in two different ways: first through their history and secondly through different scales. The first one informs about the period certain achievements and their effects like the development of new transportation technologies have lasted or in general about the time and period changes have taken place, such as the extension of docks in the course of industrialization, which may have straightened the otherwise rough coastline. The second one offers insight over which range of scale various processes act, indicated by the Richardson plots: the generally slight curved behavior of the log-log graph, which is derived from the different effects of processes - operating on different scales - on the irregularity, is sometimes interrupted by straight line sequences. These sequences expect that a certain process or better to say, a single set of processes is operating within this specific range. In general Batty and Longley consider that the fractal dimension is decreasing with scale as there is greater control on smaller scales, and that the fractal dimension on smaller scales is decreasing over time, because of greater controls over building technology and land developments - see picture 78[14].

Footnotes

[01] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 33.
[02] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 35.
[03] Statement of the painter Ben Shahn. Arnheim Rudolf, Kunst und Sehen: e. Psychologie d. schöpfer. Auges (expanded and revised edition 1978), Walter de Gruyter & Co., ISBN 3-11-006682-3, p. 93.
[04] This approach reminds us of the statement of movement of Modern Architecture: "Form follows function".
Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 42.
[05] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 44.
[06] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 43.
[07] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 58.
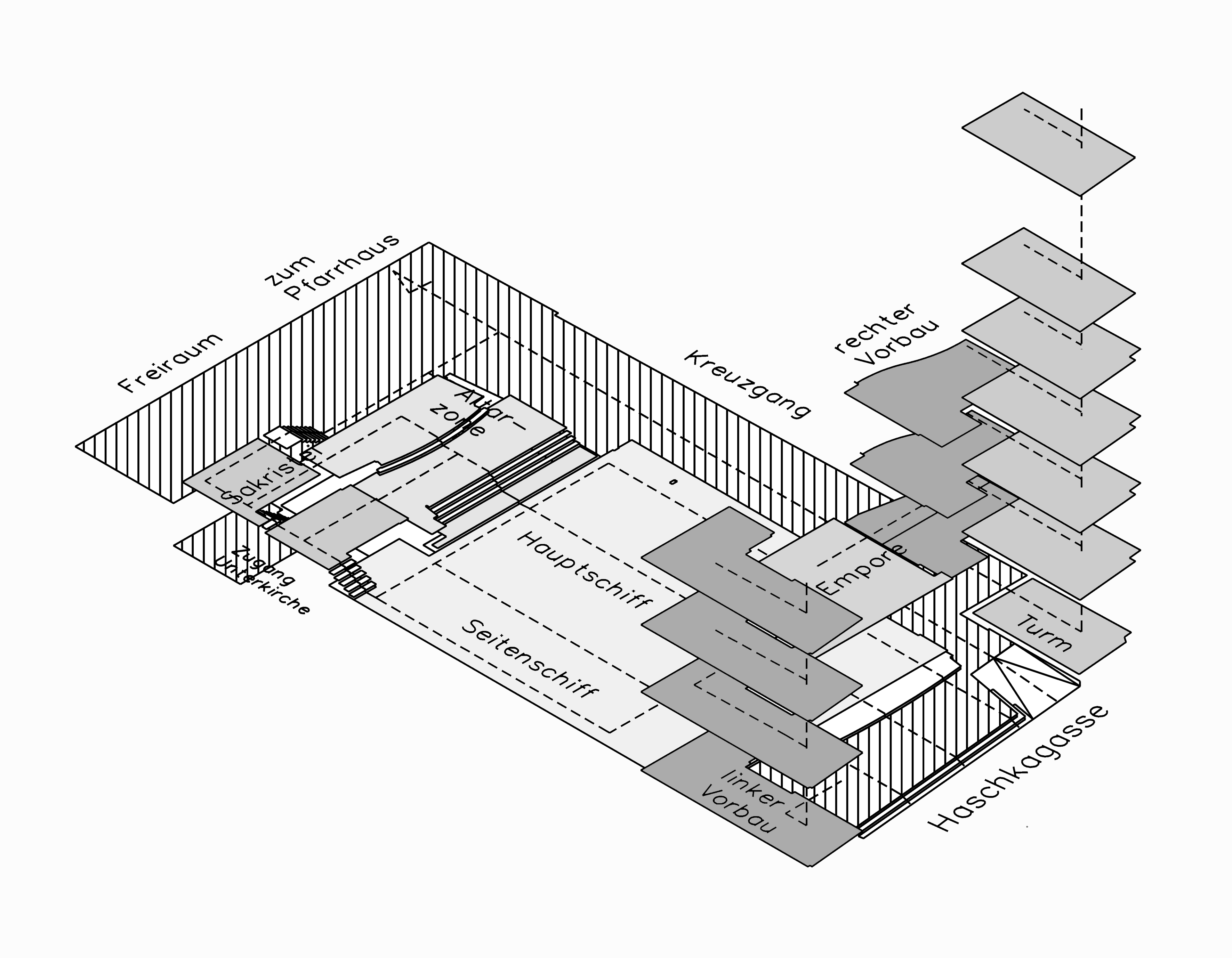
[08] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 123.
[09] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 228-229.
[10] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 272.
[11] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 165.
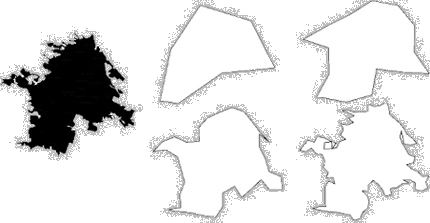
[12] Various geophysical processes influence the forms of coastlines.
[13] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 180-181.
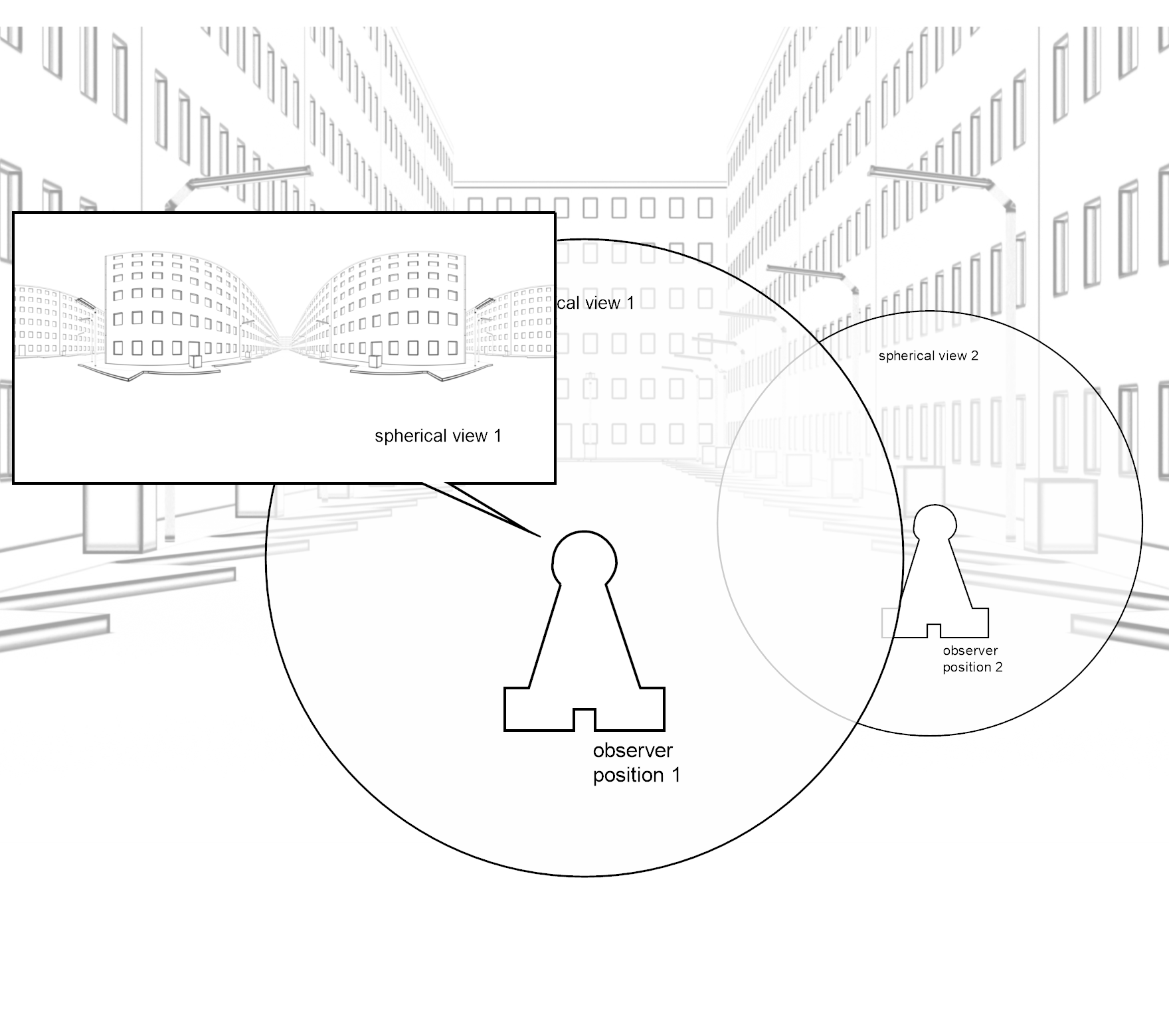
Maybe the kind of transportation system - tramway, underground, car, bus - and its availability - unbroken or fragmentary - also changes fractal dimension.
[14] Batty and Longley, Fractal Cities (1994), Academic Press Inc., ISBN 0-12-4555-70-5, p. 181.